The principle of equivalence

One important property of an inertial frame is that a particle stays at rest or moves with uniform velocity unless it is acted on by a force [ Statement of Newton's first law  ]. In the last section we discovered that bodies freely falling in a gravitational field all accelerate at the same rate regardless of their internal composition. It follows that relative to a non- rotating freely falling frame , at least locally, particles remain at rest or move in straight lines with uniform velocity, since this frame accelerates at the same rate as particles do. By locally we mean that observations are confined to a region over which the variation of the gravitational field is un- observably small. This leads to the following statement of the principle of equivalence .

• POE 1: There are no local experiments which can distinguish non- rotating free fall in a gravitational field from uniform motion in space in the absence of a gravitational field.

We conclude that a non- rotating freely falling frame is a local inertial frame. Let's check this by viewing the Pound- Snider experiment  from the view point of a freely falling frame.

Let us take the particular frame to be at rest when the photon begins its upward journey and falls freely after that. Since the photon rises a distance h, it takes a time to arrive at the top. In this time, the frame has acquired a velocity downward relative to the tower.

We can now use the redshift  formula from section 2.2 to calculate the photon's frequency relative to the freely falling frame:

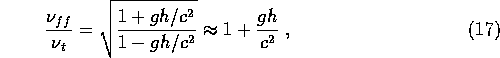
so

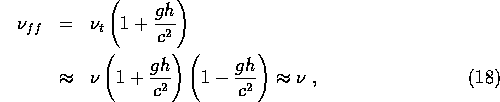
since we neglect terms of higher order [ as we did in section 2 ]. So there is no redshift in a freely falling frame thus confirming that it is a local inertial frame.

Einstein noted one other coincidence in Newtonian theory which proved to be of great importance in formulating the principle of equivalence. All inertial forces are proportional to the mass of the body experiencing the force. There is one other force which behaves like in the same way, that is the force of gravitation. For, if we drop two bodies in the earths gravitational field, then they experience forces and respectively. This coincidence suggested to Einstein that the two effects should be considered as arising from the same origin. Thus he suggested that we treat gravitation as as inertial effect as well, in other words as an effect which arises from not using an inertial frame. Comparing the force mg of a falling body with the inertial force ma suggests the following version of the principle of equivalence .

• POE 2: A frame linearly accelerated relative to an inertial frame in special relativity is locally identical to a frame at rest in a gravitational field.

These two versions of the principle of equivalence [ POE 1, POE 2 ] can be vividly clarified by considering the famous ``gedänken'' experiments of Einstein called the lift experiments .

We consider an observer confined in a lift with no windows in it or other methods of communication with the outside world. The observer is allowed equipment to carry out simple dynamical experiments. The object of the exercise is to try and determine the observers state of motion. Let us consider four cases [ see Figure 5.4 ].

 

Figure 5.4: The lift experiments

• Case 1: The lift is placed in a rocket ship in a part of the universe far removed from gravitating bodies. The rocket is accelerated forward with a constant acceleration g relative to an inertial observer. The observer releases a body from rest and sees it fall to the floor with acceleration g.
• Case 2: The rocket motor is switched off so that the lift undergoes uniform motion relative to the inertial observer. A released body is found to remain at rest relative to the observer in the lift.
• Case 3: The lift is next placed on the surface of the earth, whose rotational and orbital motions are ignored. A released body is found to fall to the floor with acceleration g.
• Case 4: Finally, the lift is placed in an evacuated lift shaft and allowed to fall freely towards the center of the earth. A released body is found to remain at rest relative to the observer.

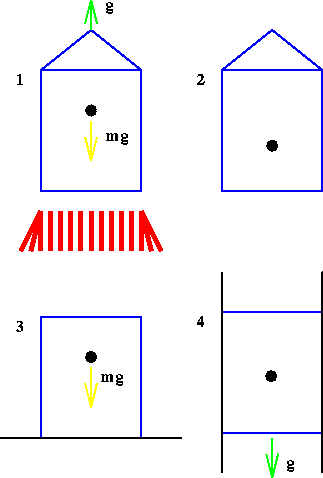
Clearly, from the point of view of the observer in the lift, cases 1 and 3 are indistinguishable, as required by POE 2, and cases 2 and 4 are indistinguishable, as required by POE 1.

This is the principle of equivalence  between gravity and acceleration, and is a corner stone of the theory of General Relativity. In more modern terminology, what we have described is called the weak equivalence principle , ``weak'' because it refers only to gravity. We shall later use the strong equivalence principle , which says that one can discover how all the laws of physics behave in a gravitational field by postulating that their laws in a freely falling inertial frame are identical to their laws in Special Relativity i.e. when there are no gravitational fields.